by Pawel Danielewicz

Neutron stars represent collapsed interiors of massive stars that reached the end of their life.  During an explosion leading to neutron star formation many elements are formed, that exist in our surrounding and are incorporated into our bodies.  Neutron stars represent the most dense objects that persist in Nature and they persist on the verge of imploding into a black hole.  The density in the interior of neutron stars is several times as high as that in the interior of atomic nuclei where practically all mass of atoms is concentrated.  In contrast to nuclei, where the numbers of constituent protons and neutrons tend to be similar, neutron stars contain far more neutrons than protons, hence the name.

To understand the formation and structure of neutron stars, it is necessary to understand how nuclear properties and, in particular, energy evolve with nuclear density and with neutron-proton imbalance.  Given known invariance of nuclear interactions under neutron-proton interchange, the nuclear energy can be expanded quadratically in neutron-proton imbalance, whether for nuclei or for matter in the interior of neutron stars,.  The coefficient of expansion, generally depends on the net number of nucleons A in the case of a nucleus and on the net density of nucleons rho in the case of matter in a neutron star.  In the case of matter, the expansion coefficient S(rho) is called the symmetry energy and in the case of nucleus the expansion coefficient a_a(A) is called the symmetry coefficient.  The two are interdependent as density varies across nuclei from low in the surface to the highest in the central nuclear region.  Because different nuclei have different proportions of central to surface regions, with heavy nuclei having relatively more of the central region and with light having less, the coefficient a_a varies with the number A.  By selectively studying nuclear excitation spectra, Danielewicz and Lee [1] deduced the coefficient a_a for individual nuclei, see Fig. 1.  The observed dropping of the coefficient with dropping nucleon number A may be understood in terms of dropping S with dropping density rho and in terms of larger surface contributions with low rho in lighter nuclei.  By comparing the results on a_a(A) with theoretical calculations of nuclear energies tied to different S(rho), Danielewicz and Lee were able to deduce constraints on S(rho) for densities encountered in nuclei.  These serve as a basis for extrapolations to densities encountered in neutron stars.

[1]  Pawel Danielewicz and Jenny Lee, Nucl. Phys. A 922, 1 (2014).

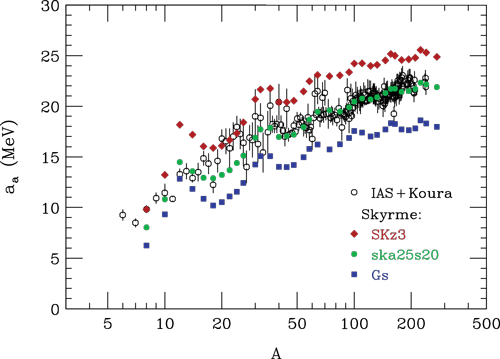
Fig. 1: Symmetry coefficients a_a for nuclei with nucleon number A.  Open circles show coefficient values deduced [1] from nuclear excitation spectra.  Lines show theoretical predictions for the coefficients.

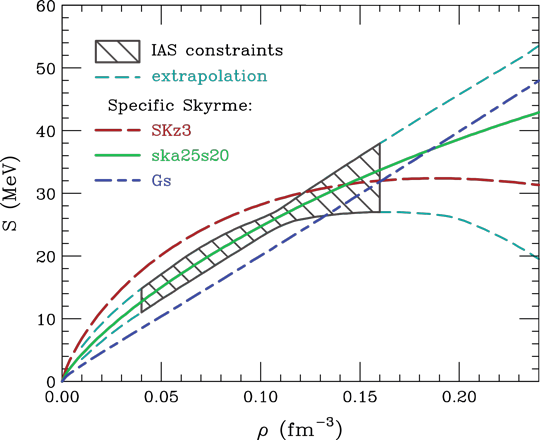
Fig. 2:  Symmetry energy S as a function of nuclear density rho.  Shaded region represents constraints deduced from a_a(A).  Lines show S(rho) for selected theoretical models.