Hidden symmetry explained
Nucleons can have two possible spins (up or down) and two different varieties or isospins (proton or neutron). The forces among the nucleons in an atomic nucleus are complicated since nucleons are built from more fundamental components known as quarks and gluons. In some cases, however, the nuclear force reveals itself to be simple and symmetrical, as though the distinction between spin and isospin is lost. Eugene Wigner first studied such approximate symmetries of the nuclear force many years ago. In “Hidden spin-isospin exchange symmetry”, Phys. Rev. Lett. 127, 062501 (2021), the authors show that the interchange of spin and isospin is an accurate symmetry of the nuclear force when averaging over spin orientations and explain why this symmetry often remains hidden from view.
The force that binds quarks and gluons is generated by a theory called quantum chromodynamics. The individual pieces carry ”colors” that are bound to form colorless objects such as nucleons. Previously, it had been shown that the structure of the nucleon simplifies when the number of colors is large. The nucleon spin and isospin arise from quark spin and isospin combinations that mirror one another. This results in a spin-isospin exchange symmetry where one can swap spin and isospin labels (up/down and proton/neutron).
There is, however, a “Goldilocks effect” associated with this symmetry. If one probes the nucleon at energies that are too low or too high, the conditions for the exchange symmetry are no longer valid. The authors demonstrate the accuracy of this symmetry for shell model calculations of atomic nuclei and deduce a priori which of the three-nucleon forces are more important than others in high-density environments such as the interior of neutron stars.
The research was carried out by FRIB theorists D. Lee, S. Bogner, B.A. Brown, H. Hergert, and M. Hjorth-Jensen, working with collaborators in Germany, China, and Turkey.
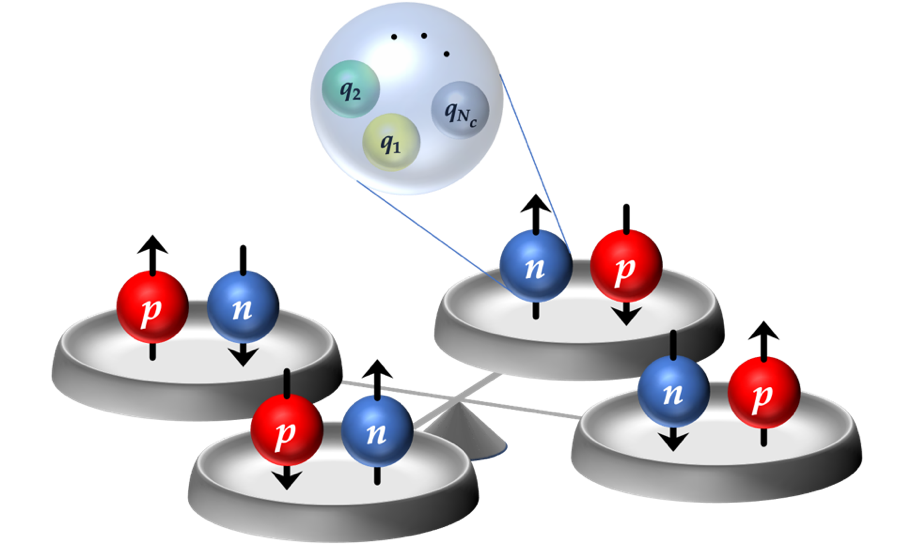
Figure: Spin-isospin exchange symmetry in the limit that the number of colors is large.



