Quantum Wave Functions Computed Faster

One of the most challenging problems in theoretical science is computing the quantum wave function of a strongly interacting system with many particles.  To help address this challenge, eigenvector continuation is a computational method that approximates the wave function by taking advantage of its smooth dependence upon some control parameter, c, such as the strength of the particle interactions.  The basic strategy is to approximate the desired wave function as a linear combination of wave functions corresponding to several training points.  The simple strategy has proven to be quite useful and widely adopted to improve calculations of quantum wave functions and scattering.

In “Convergence of Eigenvector Continuation” by Sarkar and Lee, recently published in Phys. Rev. Lett. 126, the authors present the first study of the convergence of eigenvector continuation.  They compare the performance of eigenvector continuation to that of perturbation theory, where one computes an expansion in powers of c. 

The authors find that eigenvector continuation converges more rapidly than perturbation theory and explain how this faster convergence is achieved.  In perturbation theory, there is an inherent inefficiency due to higher derivatives of the wave function not being orthogonal to lower derivatives of the wave function.  This causes a substantial amount of interference between terms.  In contrast, eigenvector continuation operates by finding the optimal linear combination of wave functions corresponding to the training points, and the problem is eliminated.  This explains the accelerated convergence of eigenvector continuation in applications such as nuclear structure calculations and probing the connection between nuclear forces and structure.  Such studies will help explain which forces are most relevant to the binding of very neutron-rich nuclei such those expected to be discovered at the Facility for Rare Isotope Beams. 

 

 

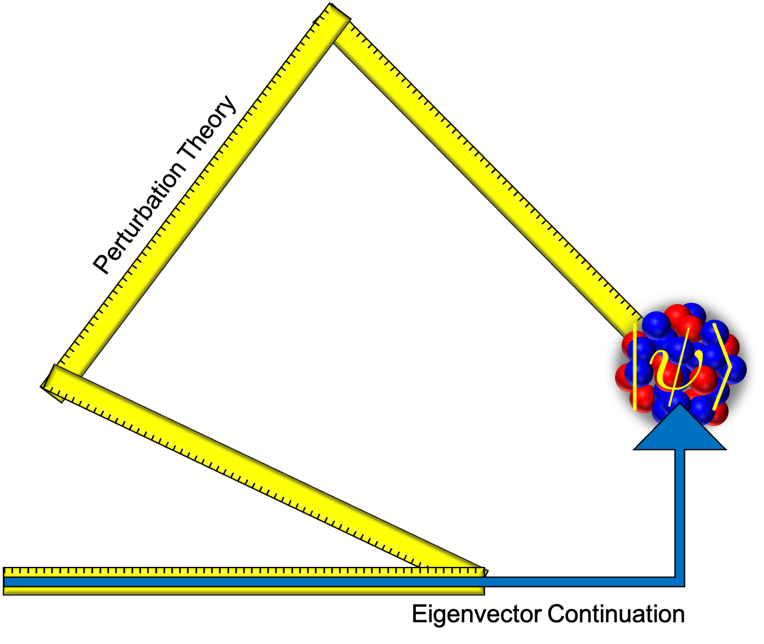
Figure:  Calculations of the quantum wave function using perturbation theory and eigenvector continuation.  The faster convergence of eigenvector continuation is due to the orthogonality of the individual steps.