Mirror Charge Radii and the Neutron Equation of State
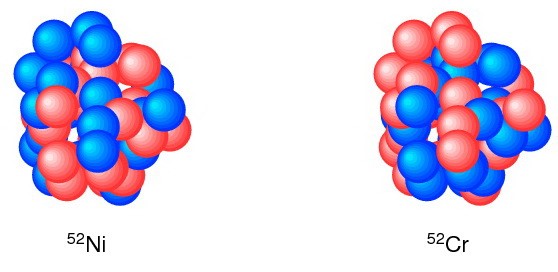
Mirror nuclei are those with the same atomic number but with the numbers of protons and neutrons interchanged. The figure shows an example for A=52 that compares chromium-52 with Z=24 protons and 28 neutrons with nickel-52 with Z=28 protons and 24 neutrons. Due to the isospin symmetry of the nuclear force, the properties of these two nuclei are nearly identical except that the protons (red) and neutrons (blue) are interchanged.
A 'neutron skin' is the difference between the root-mean-square (rms) radii of neutrons and protons in a neutron-rich nuclei such as chromium-52. A measurement of the neutron skin is important since it determines the derivative of the neutron matter equation of state (EOS), which is needed to understand global properties of neutron stars.
The proton rms radius can be determined very precisely by the electromagnetic interaction of electrons with the protons in the nucleus. Parity-violating electron scattering experiments can determine the neutron rms radius (via the exchange of a Z boson), but the error from such experiments is still very large.
When there is exact mirror symmetry, the proton rms radius in the mirror nucleus nickel-52 is equal to the neutron rms radius in chromium-52. This, together with the previously measured proton radius of chromium-52, determines the neutron skin. However, the mirror symmetry is partly destroyed by the Coulomb interaction between protons in the nucleus and other isospin-breaking effects. A recent paper has pointed out that the Coulomb interaction distorts the neutron skin with the addition of a term that depends on the value of the neutron matter EOS. This extra term becomes important when the difference in the number of neutrons and protons (N-Z) becomes small. But the difference in the mirror proton rms radii remains a robust measure of the derivative. The paper points out several possibilities for new measurements at the NSCL and FRIB that can be made with laser spectroscopy techniques.



