Probing the neutron star structure with a radioactive 22Mg beam

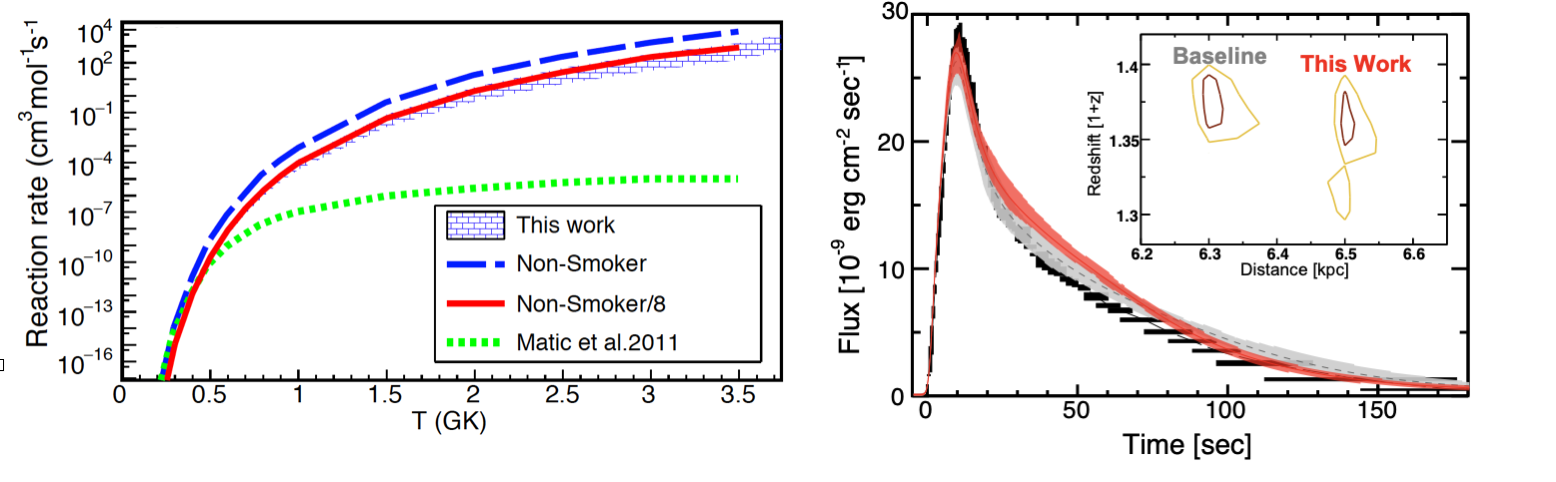
Observations of X-ray bursts on the surface of a neutron star, that accretes material from a companion donor star in a binary system, open up a new window to understand these difficult-to-size-up systems. The accreted material is burned via nuclear reactions. This generates energy which is released as X-rays. The amount of produced energy as a function of time, called light curve, is observed via space-based X-ray telescopes. Since the X rays emitted on the surface are affected by the strong gravity of the massive neutron star (surface gravitational redshift), it changes the shape of the light curve. Therefore, a model-observation comparison allows isolating the effect of gravity, hence putting constraints on the neutron star compactness (mass-radius relationship). However, such studies are limited by the uncertainty in the nuclear reaction rates that power the burst. A few reaction rates directly impact the energy generation and hence change the modeled light curves significantly. Various sensitivity studies have shown that the ²²Mg(alpha,p)²⁵Al reaction rate directly impacts the light curves, proving its determination critical for the model-observation comparisons. 

Direct measurements of this crucial reaction are very challenging due to the low intensity of a  ²²Mg rare-isotope beam. Active targets provide an ample tool to carry out such experiments with comparably low-intensity beams. Recently, an experiment was performed to directly measure this reaction cross section using the Active Target Time Projection Chamber (AT-TPC) and a re-accelerated ²²Mg beam from the ReA3 facility at NSCL. The AT-TPC was filled with helium gas which acts both as the target and the detector medium. The AT-TPC was placed inside the 2 Tesla magnetic field of a solenoid magnet. ²²Mg impinged on the ⁴He and the protons resulting from the (alpha,p) reaction were detected by tracking their spiral trajectories in the magnetic field. As described in the recent Phys. Rev. Lett. paper by NSCL team, the new reaction rate is a factor of 10 lower than the previous theoretical predictions used in light-curve modeling. The new measurement suggests a less compact neutron star in the most studied neutron star binary system GS1826-24; it removes a significant uncertainty in the model-observation comparison of X-ray bursts.

 

Phys. Rev. Lett. 125, 202710 (2020)