Research by Filomena Nunes
Optical potentials in nuclear reactions
by Filomena Nunes
Nuclear reactions are an important probe to understanding the matter we are made of. Often only a few nucleons participate actively in the reaction process, and therefore it is reasonable to freeze many of the degrees of freedom and translate the problem into a few-body problem. In doing that, one introduces effective interactions.
Say we take for example the single-neutron transfer reaction A(d,p)B, where the neutron inside the deuteron gets pulled into the target nucleus when flying close to the target. We can study this reaction as a three-body process involving a neutron, a proton and the target A. While treating the three-body scattering problem is easier than the many-body scattering, it introduces effective interactions between the neutron/proton and the target. These interactions need to account for all the physics that is not explicitly included in our three-body model, particularly the possibility of target excitation and breakup. This is achieved by introducing an imaginary component in the interaction, which acts like a sink that removes flux. These interactions are often referred to as optical potentials.
Traditionally, optical potentials have been determined through fitting data – mostly elastic scattering data N+A->N+A. However this fitting procedure introduces ambiguities and requires the existence of data. When we move away from stability, often this data is unavailable. It has therefore become clear that a microscopic description of the optical potential is crucial to provide guidance to extrapolations into the unknown regions. We do understand that optical potentials derived microscopically are intrinsically non-local. We have been working toward extending reaction theory to handle non-locality. We have demonstrated the importance of non-locality in (d,p) reactions. We are now working towards extracting optical potentials from many-body theories that include many-body correlations, and have a correct treatment of the continuum. In doing this we hope to learn more about the systematics in these effective interaction as we move far from stability. This knowledge will greatly reduce current uncertainties in the predictions of reaction observables.
Dispersive Optical Model optical potential for protons on 40Ca at 50 MeV: real part (top) and imaginary part (bottom). While a local potential depends only on the distance between projectile and target, a non-local potential has an additional radial dependence.
Describing compound reactions for neutron capture
by Filomena Nunes
The deuteron is composed of one proton and one neutron, and is a stable particle. Deuteron reactions have long been used to study nuclear structure. One common reaction of interest is when the deuteron loses its neutron and flies out as a proton – the so-called transfer reaction represented by (d,p). During the reaction process, the neutron might have been absorbed by the target to form a bound state in a direct process, or hung out around the target forming a compound nucleus that then decays.
While theorists have paid a lot of attention to the first, the description of the compound contribution has not been advanced for decades. This part of the process has societal benefits as it is used indirectly to extract information on neutron-induced reactions for stockpile stewardship – the surrogate method. It is also of interest to astrophysics in connection with the rapid neutron-capture process.
Recently, a theoretical formalism that aims at describing the (d,p) reaction mechanism has been developed, integrating consistently both direct and compound contributions. The theory is able to predict energy distributions of the detected proton for the (d,p) reaction, for energies in which the final neutron is not bound to the target. In the figure, the results for Niobium-93(d,p) at deuteron energies of 15 MeV and 25 MeV are shown. The predicted total cross section (solid line) is a result of both, elastic breakup (dot-dashed line) and other inelastic processes (dashed line). Theory is compared to the data (dots), demonstrating that the model provides a good description of process, especially at 15MeV.
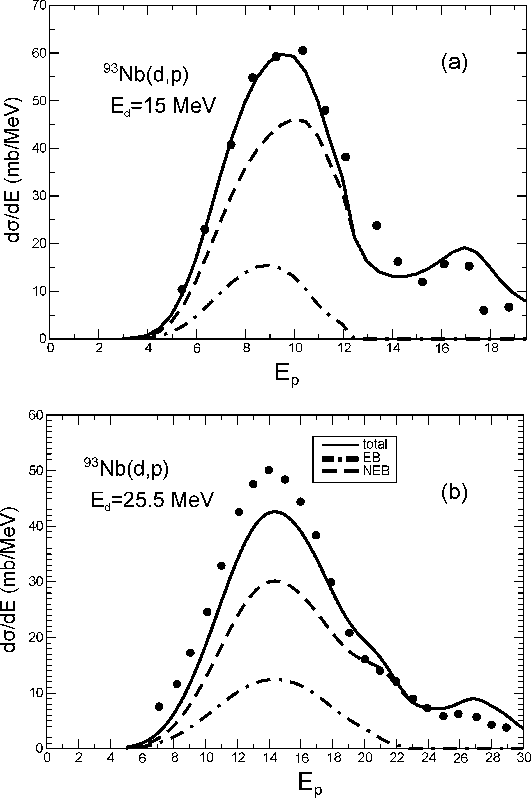
Figure: Energy distributions of the detected proton for the (d,p) process on 93Nb at 15 MeV and 25 MeV. The total cross section (solid line) is a result of elastic breakup (dot-dashed line) and the inelastic processes (dashed line). Copyright Phy. Rev. C 92, 034611 (2015).



